Antiderivadas
Um físico que conhece a velocidade de uma partícula pode desejar saber sua posição em um dado instante. Um engenheiro que pode medir a taxa de variação segundo a qual a água está escoando de um tanque quer saber a quantidade escoada durante um certo período de tempo. Um biólogo que conhece a taxa segundo a qual uma população de bactérias está crescendo pode querer deduzir qual o tamanho da população em certo momento do futuro. Em cada caso, o problema é encontrar uma função F cuja derivada é uma função conhecida f. Se a função F existir, ela é chamada uma antiderivada de f.
Definição Uma função F é chamada um antiderivada de f sobre um intervalo I se F’(x)=f(x) para todo x em I
Por exemplo, encontre uma antiderivada de f(x) = x2. Lembrando a regra da potência, se F(x) = 1/3 x3 , então F’(x) = x2 = f(x). Mas a função G(x) = 1/3 x3 +100 também satisfaz G’(x) = x2 = f(x). Conseqüentemente, ambas F e G são antiderivadas de f. Na verdade, qualquer função da forma H(x) = 1/3 x3 + C, onde C é uma constante, é uma antiderivada de f.
Teorema Se F for uma antiderivada de f em um intervalo I, então a antiderivada mais geral de f em I é:
F(x) + C
onde C é uma constante arbitrária.
Exemplo 1 Encontre uma antiderivada mais geral de cada uma das seguintes funções:
a)

b)

c)
 , n<>1
, n<>1
Exemplo 2 Encontre todas as funções de g tal que:

Nas aplicações de cálculo é muito comum situações como este exemplo, onde é requerido achar uma função sendo fornecidos dados sobre suas derivadas. uma equação que envolva as derivadas de uma função é chamada de equação diferencial. A solução geral de uma equação diferencial envolve uma constante arbitrária, contudo, podem ser dadas condições extras que irão determinar as constantes e assim especificar univocamente a solução.
Exemplo 3 Encontre f se  e
e 
Exemplo 4 Encontre f se 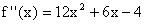 ,
,  e
e 
Movimento Retilíneo
Antidiferenciação é particularmente útil na análise do movimento de um objeto que se move em uma reta. Lembre-se que a função posição s(t) = f(t), então a função velocidade v(t) = s’(t). Da mesma maneira, a função aceleração é a(t) = v’(t). Se a aceleração e os valores iniciais s(0) e v(0) são conhecidos, então a função posição pode ser encontrada antidiferenciando-se duas vezes.
Exemplo 5 Uma partícula move-se em uma reta e tem aceleração dada por a(t) = 6t + 4. Sua velocidade inicial é v(0) = -6 cm/s, e seu deslocamento inicial é s(0) = 9 cm. Encontre sua função posição s(t).
Exemplo 6 Uma bola é arremessada para cima com uma velocidade de 48 pés/s da margem de um penhasco 432 pés acima do solo. Encontre sua altura acima do solo t segundos mais tarde. Quando ela atinge sua altura máxima? Quando atinge o solo?
Exercícios
a)
Encontre a antiderivada mais
geral da função 
b)
Encontre a antiderivada F de
f que satisfaça a condição dada:  ,
, 
c)
Encontre f se 
d)
Encontre f se  ,
,  ,
, 
e)
Encontre f se  ,
,  ,
,  ,
, 
f) Uma pedra é deixada cair do posto de observação de uma torre, 450 pés acima do solo. Determine quanto tempo leva para a pedra atingir o solo? Com que velocidade ela atinge o solo?